Circle X Is Shown in the Diagram. Which Equation Can Be Used to Solve for Mã¢ë†â 1?

Logistic Map

Replacing the logistic equation
| | (i) |
with the quadratic recurrence equation
| | (two) |
where (sometimes also denoted
) is a positive constant sometimes known every bit the "biotic potential" gives the so-chosen logistic map. This quadratic map is capable of very complicated behavior. While John von Neumann had suggested using the logistic map
every bit a random number generator in the late 1940s, it was not until work by Westward. Ricker in 1954 and detailed analytic studies of logistic maps beginning in the 1950s with Paul Stein and Stanislaw Ulam that the complicated properties of this type of map beyond elementary oscillatory behavior were widely noted (Wolfram 2002, pp. 918-919).
The first few iterations of the logistic map (2) give
where is the initial value, plotted above through five iterations (with increasing iteration number indicated past colors; i is scarlet, ii is yellowish, iii is dark-green, 4 is blue, and 5 is violet) for various values of
.
The logistic map computed using a graphical procedure (Tabor 1989, p. 217) is known as a web diagram. A web diagram showing the first hundred or so iterations of this process and initial value
appears on the cover of Packel (1996; left figure) and is animated in the correct figure higher up.
In general, this recurrence equation cannot be solved in closed form. Wolfram (2002, p. 1098) has postulated that any verbal solution must be of the form
| | (6) |
where is some part and
is its inverse function. Thou. Trott (pers. comm.) has shown that smooth solutions cannot exist for generic values of
, with the possible exception of
fifty-fifty and nonzero. The only exact solutions known are for r=-two, r=2 and r=4, summarized in the tabular array below (Wolfram 2002, p. 1098), and R. Germundsson (pers. comm., Apr. 25, 2002) has proved that no other solutions of this form are possible.
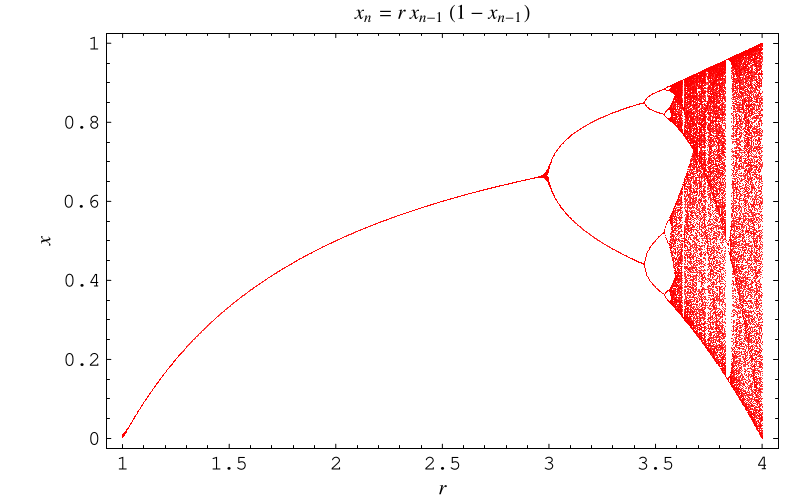
The illustration above shows a bifurcation diagram of the logistic map obtained by plotting as a part of a serial of values for
obtained by starting with a random value
, iterating many times, and discarding the commencement points corresponding to values before the iterates converge to the attractor. In other words, the gear up of fixed points of
corresponding to a given value of
are plotted for values of
increasing to the right.
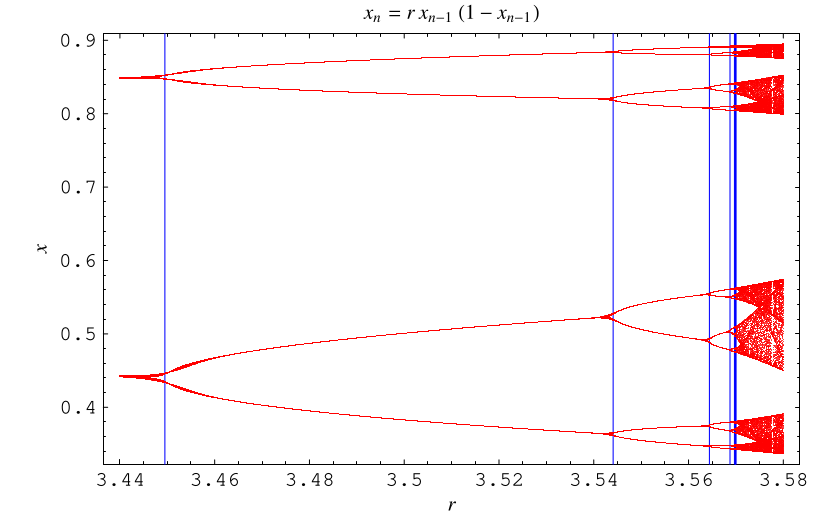
An enlargement of the previous diagram around is illustrated in a higher place, with value of
at which a
-bike first appears indicated past blueish lines.
In society to report the fixed points of the logistic map, permit an initial point lie in the interval
. Now find appropriate weather on
which proceed points in the interval. The maximum value
tin can accept is found from
| | (7) |
then the largest value of occurs for
. Plugging this in,
. Therefore, to continue the map in the desired region, we must have
. The Jacobian is
| | (eight) |
and the map is stable at a point if
.
Now find the fixed points of the map, which occur when . For convenience, drib the
subscript on
| | (9) |
| | (10) |
then the stock-still points are and
.
An interesting matter happens if a value of greater than iii is called. The map becomes unstable and we get a pitchfork bifurcation with two stable orbits of period two corresponding to the ii stable fixed points of
. The stock-still points of club two must satisfy
, so
For convenience, drop the subscripts and rewrite
Notice that nosotros have establish the start-order fixed points besides, since two iterations of a beginning-guild fixed indicate produce a trivial 2d-order fixed point. The truthful 2-cycles are given past solutions to the quadratic part
These solutions are simply real for , and then this is where the 2-wheel begins. Note that the 2-cycle can also exist plant past computing the discriminant of
| | (22) |
which is
| | (23) |
When this equals 0, two roots coincide, so is the onset of period doubling. For
, the solutions
are given by (0, 0,
) and (
,
, 3), so the beginning bifurcation occurs at
.
In full general, the set of equations which tin be solved to requite the onset of an arbitrary
-wheel (Saha and Strogatz 1995) is
 | (24) |
The first of these give
,
, ...,
, and the last uses the fact that the onset of period
occurs past a fold bifurcation, and so the
th derivative is i. For pocket-size
, these tin be solved exactly, but the complexity rapidly increases with
.
Now look for the onset of the three-bicycle. To eliminate the ane-cycles, consider
| | (25) |
This gives
| | (26) |
The roots of this equation are all imaginary for less than some cutoff
, at which point two of them convert to real roots. The value of
can be institute by computing the discriminant of (26),
 | (27) |
When the discriminant is zip, two roots coincide. This happens at
| | (28) |
(OEIS A086178) as first shown by Myrberg in 1958, so the 3-wheel starts at . Saha and Strogatz (1995) give a simplified algebraic treatment for the 3-wheel which involves solving
| | (29) |
together with 3 other simultaneous equations, where
Further simplifications still are provided in Bechhoeffer (1996) and Gordon (1996), simply neither of these techniques generalizes easily to higher cycles. Bechhoeffer (1996) expresses the three boosted equations as
giving
| | (36) |
This has the positive solution found previously, .
Gordon (1996) derives not only the value for the onset of the 3-cycle, just also an upper jump for the
-values supporting stable catamenia-iii orbits. This value is related to the unique positive root
of the cubic equation
| | (37) |
by
| | (38) |
which is the unique positive root of the sextic polynomial
(OEIS A086179). For ,
Solving the resulting cubic equation using estimator algebra gives
| | (44) |
and ,
,
given by
| | (45) |
giving numerical roots
where is the silvery constant.
To observe the onset of the 4-cycle, eliminate the 2- and i-cycles by considering
 | (56) |
This gives a 12th-order polynomial in . The value of
can be found past computing the discriminant of this polynomial,
 | (57) |
whose only real positive roots are
The 4-cycle therefore starts at
| | (62) |
(OEIS A086180).
The onset of 5-cycles tin be institute analytically, and gives a 22nd-social club polynomial in whose real positive roots are
(OEIS A118452), 3.90557..., and 3.99026....
The onset of 6-cycles can be found analytically, and gives a 40th-order polynomial in whose real positive roots are
(OEIS A118453), 3.93751..., 3.97776..., and 3.99758....
The onset of seven-cycles tin be constitute analytically, and gives a 114th-order polynomial in whose existent positive roots are
(OEIS A118746), 3.77413..., 3.88602..., 3.92218..., 3.95102..., 3.96897..., 3.98474..., 3.99453..., and 3.99939....
The onset of viii-cycles can be found analytically as the polynomial root of the 8th-order polynomial
(OEIS A086181; Bailey 1993; Bailey and Broadhurst 2000; Borwein and Bailey 2003, pp. 51-52).
The onset of 16-cycles at (OEIS A091517) was originally found using an integer relation adding which determined that
is the root of a 120th-degree integer polynomial with coefficients that decrease monotonically from
to ane (Bailey and Broadhurst 2000; Borwein and Bailey 2003, pp. 52-53). This consequence was afterwards verified exactly using computer algebra (Borwein and Bailey 2003, p. 53; Kotsireas and Karamanos 2004), and is an algebraic number of degree 240.
The following table summarizes the values at which the
-cycle start appears. For
, 2, ..., these have algebraic degrees 1, ane, 2, 2, 22, xl, 114, 12, ... (OEIS A118454).
The algebraic orders of the values of (i.e., the onset of the
-wheel) for
, two, ... are therefore given past one, 2, 12, 240, ... (OEIS A087046). A table of the bike type and value of
at which the cycle
appears is given below.
For boosted values, run into Rasband (1990, p. 23). Note that the table in Tabor (1989, p. 222) is wrong, as is the entry in Lauwerier (1991). The menstruum doubling bifurcations come faster and faster (8, 16, 32, ...), then suddenly break off. Beyond a certain bespeak known as the aggregating point, periodicity gives way to chaos, as illustrated beneath. In the middle of the complexity, a window suddenly appears with a regular period similar three or 7 as a result of mode locking. The menstruation-3 bifurcation occurs at
, and period doublings and then begin once again with cycles of vi, 12, ... and 7, fourteen, 28, ..., and then one time once again break off to anarchy. Notwithstanding, annotation that considerable construction can exist found inside this chaos (Mayoral and Robledo 2005ab).
It is relatively piece of cake to show that the logistic map is chaotic on an invariant Cantor ready for (Devaney 1989, pp. 31-50; Gulik 1992, pp. 112-126; Holmgren 1996, pp. 69-85), only in fact, information technology is as well chaotic for all
(Robinson 1995, pp. 33-37; Kraft 1999).
The logistic map has correlation exponent (Grassberger and Procaccia 1983), chapters dimension 0.538 (Grassberger 1981), and information dimension 0.5170976 (Grassberger and Procaccia 1983).
The logistic map can exist used to generate random numbers (Umeno 1998; Andrecut 1998; Gonzáles and Pino 1999, 2000; Gonzáles et al. 2001ab; Wong et al. 2001, Trott 2004, p. 105).
See also
2x modern one Map, Bifurcation, Feigenbaum Constant, Logistic Map--r=2, Logistic Map--r=2, Logistic Map--r=four, Period Three Theorem, Quadratic Map, Argent Constant, Tent Map
Explore with Wolfram|Alpha
References
Bailey, D. H. "Multiprecision Translation and Execution of Fortran Programs." ACM Trans. Math. Software 19, 288-319, 1993. Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. "Bifurcation Points in Chaos Theory." §ii.iii.2 in Experimental Mathematics in Action. Wellesley, MA: A K Peters, pp. 33-36, 2007. Bailey, D. H.; Borwein, J. Thou.; Kapoor, V.; and Weisstein, E. Due west. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006. Bailey, D. H. and Broadhurst, D. J. "Parallel Integer Relation Detection: Techniques and Applications." Math. Comput. 70, 1719-1736, 2000. Bechhoeffer, J. "The Nascency of Flow 3, Revisited." Math. Mag. 69, 115-118, 1996. Beck, C.; and Schlögl, F. Thermodynamics of Cluttered Systems. Cambridge, England: Cambridge University Printing, 1993. Bogomolny, A. "Chaos Creation (There is Order in Chaos)." http://www.cut-the-knot.org/blue/chaos.shtml. Borwein, J. and Bailey, D. "Bifurcation Points in the Logistic Iteration." §2.iii in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. fifty-53, 2003. Costa, U. M. S.; Lyra, K. L.; Plastino, A. R.; and Tsallis, C. "Power-Constabulary Sensitivity to Initial Weather condition Within a Logistic-Similar Family of Maps: Fractality and Nonextensivity." Phys. Rev. East 56, 245-250, 1997. Devaney, R. An Introduction to Chaotic Dynamical Systems, second ed. Redwood Metropolis, CA: Addison-Wesley, 1989. Dickau, R. K. "Bifurcation Diagram." http://mathforum.org/avant-garde/robertd/bifurcation.html. Elaydi, S. North. Detached Chaos. Boca Raton, FL: Chapman & Hall, 2000. Gleick, J. Anarchy: Making a New Scientific discipline. New York: Penguin Books, pp. 69-80, 1988. Gordon, W. B. "Period Three Trajectories of the Logistic Map." Math. Mag. 69, 118-120, 1996. Grassberger, P. "On the Hausdorff Dimension of Fractal Attractors." J. Stat. Phys. 26, 173-179, 1981. Grassberger, P. and Procaccia, I. "Measuring the Strangeness of Foreign Attractors." Physica D 9, 189-208, 1983. Gulick, D. Encounters with Chaos. New York: McGraw-Loma, 1992. Holmgren, R. A First Course in Discrete Dynamical Systems, 2nd ed. New York: Springer-Verlag, 1996. ![]() Jaffe, South. "The Logistic Equation: Computable Chaos." http://library.wolfram.com/infocenter/MathSource/579/. Kotsireas, I. S. and Karamanos, K. "Exact Ciphering of the Bifurcation Point
Jaffe, South. "The Logistic Equation: Computable Chaos." http://library.wolfram.com/infocenter/MathSource/579/. Kotsireas, I. S. and Karamanos, K. "Exact Ciphering of the Bifurcation Point of the Logistic Map and the Bailey-Broadhurst Conjectures." Internat. J. Bifurcation and Chaos xiv, 2417-2423, 2004. http://www.lacim.uqam.ca/~plouffe/OEIS/archive_in_pdf/costas-cecm.pdf Kraft, R. L. "Anarchy, Cantor Sets, and Hyperbolicity for the Logistic Maps." Amer. Math. Monthly 106, 400-408, 1999. Latora, V.; Rapisarda, A.; Tsallis, C.; and Baranger, M. "The Charge per unit of Entropy Increment at the Edge of Chaos." Phys. Lett. A 273, 97, 2000. Lauwerier, H. Fractals: Incessantly Repeated Geometrical Figures. Princeton, NJ: Princeton University Press, pp. 119-122, 1991. MathPages. "Airtight Forms for the Logistic Map." http://world wide web.mathpages.com/dwelling house/kmath188.htm. May, R. Thou. "Simple Mathematical Models with Very Complicated Dynamics." Nature 261, 459-467, 1976. Mayoral, E. and Robledo, A. "A Recent Appreciation of the Singular Dynamics at the Edge of Anarchy." Jan. 17, 2005a. http://arxiv.org/abs/cond-mat/0501398. Mayoral, East. and Robledo, A. "Tsallis'
Index and Mori's
Phase Transitions at Edge of Anarchy." Phys. Rev. E 72, 026209, 2005b. Packel, E. Mathematica for Mathematics Teachers. Inst. of Computation, 1996. Pearl, R. Ch. eighteen in The Biology of Population Growth. New York: Knopf, 1978. Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, pp. 585-653, 1992. Quetelet, A. and Verhulst, P. F. Annuaire de l'Académie royale des sciences de Belgique 16, 97-124, 1850. Ramasubramanian, One thousand. and Sriram, Thou. S. "A Comparative Study of Computation of Lyapunov Spectra with Different Algorithms." 17 Sep 1999. http://arxiv.org/abs/chao-dyn/9909029. Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, p. 23, 1990. Robinson, C. Stability, Symbolic Dynamics, and Chaos. Boca Raton, FL: CRC Press, 1995. Russell, D. A.; Hanson, J. D.; and Ott, E. "Dimension of Strange Attractors." Phys. Rev. Let. 45, 1175-1178, 1980. Saha, P. and Strogatz, S. H. "The Birth of Period 3." Math. Mag. 68, 42-47, 1995. Sloane, North. J. A. Sequences A086178, A086179, A086180, A086181, A087046, A091517, A098587, A118452, A118453, A118454, and A118746 in "The On-Line Encyclopedia of Integer Sequences." Strogatz, Southward. H. Nonlinear Dynamics and Chaos. Reading, MA: Addison-Wesley, 1994. Tabor, M. Anarchy and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989. Tsallis, C.; Plastino, A. R.; and Zheng, W.-M. "Power-Law Sensitivity to Initial Weather condition--New Entropic Representation." Chaos, Solitons & Fractals 8, 885-891, 1997. Trott, Thou. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 24-25, 2004. http://world wide web.mathematicaguidebooks.org/. Railroad vehicle, South. "The Dynamics of the Quadratic Map." §four.4 in Mathematica in Activeness. New York: Due west. H. Freeman, pp. 117-140, 1991. Wolfram Research, Inc. "Logistic Map." http://documents.wolfram.com/mathematica/Demos/SoundGallery/LogisticMap.html. Wolfram, Due south. A New Kind of Scientific discipline. Champaign, IL: Wolfram Media, pp. 918-921 and 1098, 2002.
Referenced on Wolfram|Alpha
Logistic Map
Cite this as:
Weisstein, Eric W. "Logistic Map." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/LogisticMap.html
Subject field classifications
Source: https://mathworld.wolfram.com/LogisticMap.html
0 Response to "Circle X Is Shown in the Diagram. Which Equation Can Be Used to Solve for Mã¢ë†â 1?"
Post a Comment